週刊こぐま通信
「代表のコラム」入試速報(5)
未測量・位置表象の出題は少ないが、難問化しやすい
第915号 2024年12月6日(金)
こぐま会代表 久野 泰可
こぐま会代表 久野 泰可

私たちが幼児期の基礎教育の中で、「数」や「図形」の理解の前提として重視している「未測量」「位置表象」に関する出題は、「数」「図形」と比べると少ないようですが、出題されると難しい課題が多いのが特徴です。手元にある16校の問題を見ると、今年の出題数は以下の通りです。
【未測量】
- 多さくらべ 2校
- 長さくらべ(個別単位) 1校
- シーソー 4校
- つりあい 1校
- 逆対応 1校
【位置表象】
- 位置の対応・記憶 2校
- 位置の移動 4校
- 位置の聞きとり 1校
- 四方からの観察 5校
こぐま会で実践している「教科前基礎教育」の内容は、次のような構成になっています。
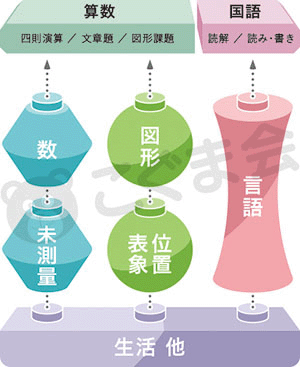
その中で、未測量と位置表象の授業内容は以下の通りです。
未測量
- step1「大きさ・多さくらべ」
- ・多さの相対化
・大きさの相対化 - step2「重さくらべ」
- ・手をつかった重さの比較
・器具をつかった重さの比較
・シーソーによる三者関係 - step3「長さくらべ 」
- ・長さの比較
・長さの相対化・系列化
・大きさと長さの順対応
・長さの個別単位 - step4「シーソー」
- ・じゃんけん・競争による三者関係
・シーソーによる三・四・五者関係
・言葉による関係推理 - step5「逆対応」
- ・ろうそく・飲んだ水の逆対応
・移しかえと元のコップの対応
・砂糖水の濃さ - step6「重さのつりあい」
- ・シーソーによる三・四・五者関係
・均衡のくずれ
・重さの一対多対応
・置き換えをつかったつりあい - step7「総合」
- ・総まとめ
位置表象
- step1「前後・上下関係」
- ・前後関係の相対化・系列化
・上下関係の相対化・系列化
・方眼上の位置の対応
・位置の記憶(つみ木・方眼) - step2「左右関係」
- ・右手・左手の理解
・交差点の曲がり方
・生活空間での位置関係 - step3「方眼上の位置と移動」
- ・右手・左手の理解(復習)
・方眼上の位置の理解
・方眼上の位置の言語化
・方眼上の位置の移動 - step4「四方からの観察(1)」
- ・四方からの具体物の写生
・カードを使った場所さがし
・いろいろなものの四方からの観察 - step5「四方からの観察(2)」
- ・四方からの観察(二者)
・反対から見たときの位置関係
・反対から見たときの写生 - step6「地図上の移動、飛び石移動」
- ・地図上の移動
・すごろく移動
・飛び石移動 - step7「総合」
- ・総まとめ
入試に直接出題されない課題であっても、将来の数や図形の基礎として大事ですので年間のカリキュラムに組み込んで学習していますが、その中で入試によく出る課題を、次のように予想したことがあります。
| 未測量 | 単位の考え方/シーソー/つりあい |
|---|---|
| 位置表象 | 左右の理解/四方からの観察/飛び石移動/地図上の移動 |
今回16校で出された問題もすべてではありませんが、予想した問題が数多く出されています。特に今回は、未測量では「つりあい」も含めて「シーソーに関する問題」が多くみられます。また位置表象では、「四方からの観察」と「移動の問題」が多かったことも判明しています。では具体的な問題を見てみましょう。
- シーソーの四者関係
- シーソーで重さくらべをしました。
-
(A) この中で2番目に重いものはどれですか。下のお部屋から選んで〇をつけてください。 (B) この中で2番目に軽いものはどれですか。下のお部屋から選んで△をつけてください。
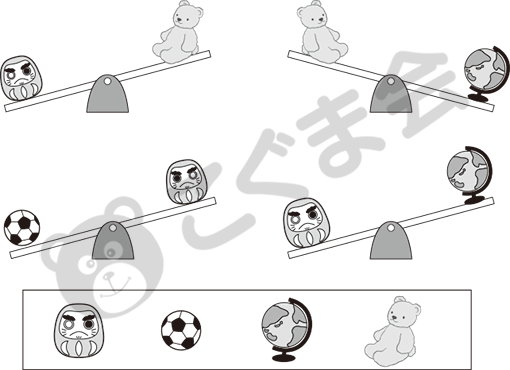
この問題は典型的な四者関係です。基本は場面は3つあればいいのですが、この問題では必要でない左上のシーソーもわざわざ入れ、4場面にして問いかけています。場面が多ければ難しくなります。今回の質問で注目していただきたいのは「2番目に重い」とか「2番目に軽い」を問いかけていることです。「一番重い」「一番軽い」だけでなく、中間が聞かれています。どんな問いかけであっても答えられることが大事です。
- シーソーのつりあい
- 上の絵を見てください。ミカン1個とイチゴ3個でつりあっています。
-
(A) ミカン1個とイチゴ1個ではどちらが下がりますか。その絵に〇をつけてください。 (B) イチゴ6個と同じ重さになるには、ミカンを何個のせたらよいですか。その数だけ〇をかいてください。
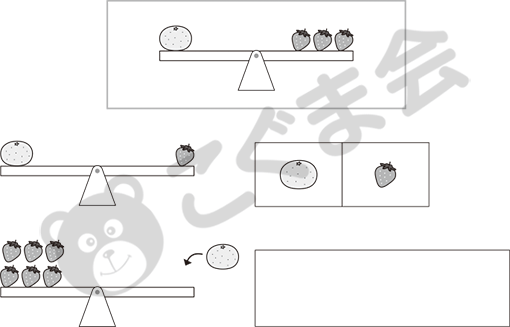
典型的なつりあいの問題です。つりあいで難しいのは「仲立ちを伴うつりあい」ですが、今回は極めて基本の問題です。(A)は1個と3個がつりあっている場合、それぞれ1個ずつではどちらが下がるかという問題です。この考え方はシーソー問題の中ではよく問われます。また(B)は、6個のイチゴの中に3個の集まりがいくつあるかという問題で、わり算の包含除の考え方につながる内容です。
次に位置表象の問題で毎年よく出されている「移動」と「四方からの観察」を見てみましょう。
- 移動の問題
-
(A) 赤い線のお部屋を見てください。ネズミは1回に2つずつ進みます。ネコは1回に1つずつ進みます。同時に進んだとき、2匹が出会うのはどこですか。その場所に〇をかいてください。 (B) 青い線のお部屋を見てください。ウサギは1回に5つずつ矢印のほうに進みます。カタツムリは1回に1つずつ矢印のほうに進みます。同時に進んだとき、ウサギはどこでカタツムリに追いつきますか。その場所に△をかいてください。
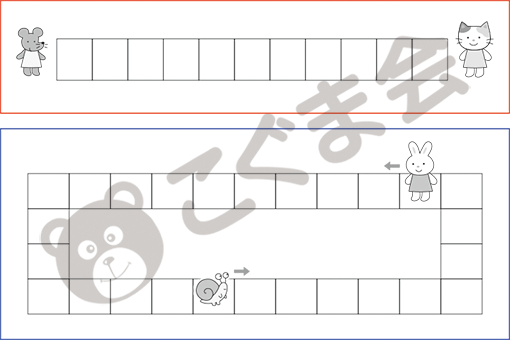
将来学ぶ「旅人算」につながる内容で、(A)は会う場所、(B)は追いつく場所を探す問題です。いずれも、実際に動かして答えを導き出す課題ですので、「動かす」作業が必要です。特に1回に1つではなく、1回に2つずつとか5つずつという移動の作業がしっかりできるかどうかが決め手です。この課題は、「飛び石移動」としていますが、移動課題には他にも「地図上の移動」「方眼上の移動」があり、今年もいくつか出されています。
- 四方からの観察の問題
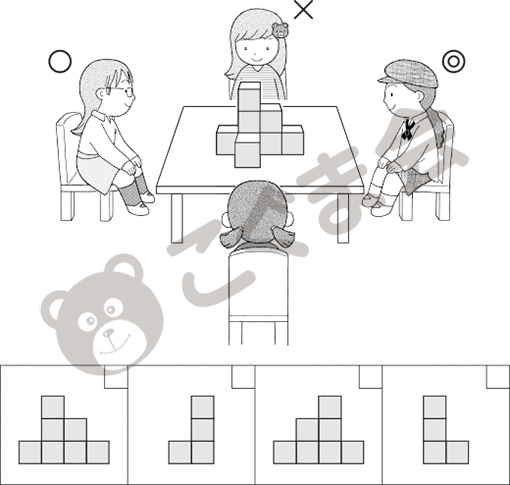
(A) 机の上のつみ木を子どもたちが見ています。それぞれどのように見えていますか。下から探して、□の中に同じ印をかいてください。
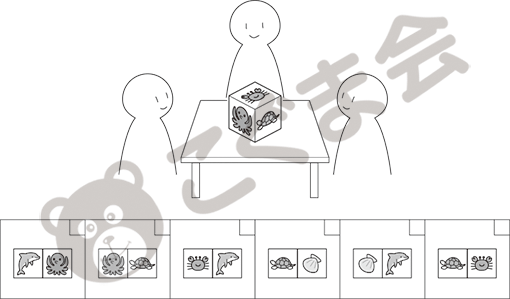
(B) 机の上のサイコロを子どもたちが見ています。サイコロの面にはそれぞれ違う生き物がかかれています。 ・奥の男の子から見える生き物はどれですか。下から探して、□の中に〇をかいてください。
| (A) | 多くの学校で出題する「つみ木を使った四方からの観察」です。選択肢には奥行きのない真四角でつみ木を表していますので、つみ木と真四角がつながるかどうか、まずそこが問われます。そのうえで特に反対側からの見え方が理解できるかどうかがポイントです。今回はありませんが、時々上から見たらどう見えるかが問われることがありますので要注意です。 |
| (B) | 四方からの観察の応用的な課題です。向こう側に描いてある絵を、右と左の人の見え方から判断しなければなりませんので、その手続きができるかどうかがポイントです。四方からの観察の問題の中で、反対からの見え方を問う問題が一番難しく、「左右関係の理解」がしっかりできているかどうかが問われます。 |
以上、今回はこぐま会で学習する「未測量」「位置表象」に関する入試問題を分析しました。まだまだ入試問題全体の中では出題数は少ないと思いますが、数や図形の問題が減る中で、この「未測量」「位置表象」の問題はいろいろ工夫されて出題数も増えていくはずですので、しっかり学習してください。
- 読み・書き・計算はまだ早い!
こぐま会代表 久野泰可 著「子どもが賢くなる75の方法」(幻冬舎)
 家庭でできる教育法を一挙公開
家庭でできる教育法を一挙公開
子どもを机に向かわせる前に実際の物に触れ、考えることで差がつく。- 食事の支度を手伝いながら「数」を学ぶ
- 飲みかけのジュースから「量」を学ぶ
- 折り紙で遊びながら「図形」を学ぶ
- 読み聞かせや対話から「言語」を学ぶ

KUNOメソッド こどもがかしこくなる絵カード(幻冬舎)
幼児の日常生活の中にある学びをカード化!
おうちで体験できるKUNOメソッド子どもたちの生活の中でできる学習経験を、ご家庭でより実践しやすいようにカード化いたしました。お求めは、SHOPこぐま・こぐま会ネットショップ ・全国の書店・各書籍ECサイトにて