週刊こぐま通信
「代表のコラム」入試速報(3)
図形課題は、いろいろ工夫され多岐にわたっている
第913号 2024年11月22日(金)
こぐま会代表 久野 泰可
こぐま会代表 久野 泰可

共学校の合格発表もほぼ終わり、問題の聞き取りも進んでいます。前回は女子校10校の「数」の問題を分析しましたが、今回は主要共学校6校を加えて、16校の「図形」課題の出題について分析します。手元にある資料に基づいて、図形の各単元のうち何がよく出されたかまとめましたので、以下の分析をご覧ください。
- 図形構成 6校
- 線対称 4校
- 同図形発見 3校
- 点図形・図形模写 3校
- 回転図形 2校
- つみ木構成 2校
- 重ね図形 2校
- 形を使った創造画 1校
- 折り紙の折れ線のつき方 1校
以前、入試でよく出される図形課題をコラム829号で次のように予想しました。
| 図形 | 図形構成―分割 / 対称図形 / 重ね図形 / 回転図形 |
|---|
今年出された問題を見ても、やはり一番多いのが図形構成です。一時期減った単元ですが、やはり小学校入試における図形問題の中心であることがはっきりしています。図形構成が少なくなった時に多く出された課題は、線対称/重ね図形/回転図形の難しい課題でしたが、今年も数は多くありませんが難しい課題として出されています。そのほか、同図形発見/点図形/図形模写のような以前からある図形課題の定番も出されています。
図形課題は、小学校算数科の図形につながる課題ですが、幼児の場合は図形の知識を覚えるというより、図形のセンスを磨くことが大事です。それが小学校の図形学習の基礎になっていくのです。その意味で、幼児の身の回りにはパズル・つみ木・折り紙といった図形感覚を育てる素材がたくさんありますので、ペーパー学習の前にそれらを使った遊びをたくさん経験させることが大事です。
前回のコラムで報告した数の問題は、四則演算につながる内容であるため問題がパターン化しやすく、オリジナルな問題を作るとなると図形課題のほうがいろいろ工夫でき、出題内容が多岐にわたっているのだと思います。ただ今後も、図形構成/つみ木構成といった「構成課題」が中心になっていくはずですので、そこを中心に家庭学習を進めていくのが良いと思います。そのうえで、線対称/重ね図形/回転図形といった新傾向の問題をしっかり学習することが大事です。合否を分ける課題が、これまでの「数」から「図形」に代わってきたことは確実に言えることです。「図形課題」に苦手意識を持たないよう、楽しく学ぶ工夫をしてください。素材がたくさんありますから、楽しく学習できるはずです。ペーパーを使っての練習はそのうえで行うことが大事です。
では、今年出された図形問題のいくつかをご紹介しましょう。
- 図形構成の問題
-
- 上の絵の黒いところに入る形はどれですか。それぞれ下から選んで○をつけてください。

パズルのピースを当てはめる課題です。色と形を考えて選択するのですが、入れるべきピースが同じ向きに置かれていれば簡単ですが、選ぶピースが回転していますので、今はやりの回転の要素が入った図形構成としてやや難しい問題です。
- 線対称
- イチゴのお部屋で練習してみましょう。左の形は透明な紙にかかれています。これを太い線のところで矢印のほうに折って重ねると、中の形は〇のついているところに来ます。
- リンゴのお部屋を見てください。同じように、左の形を太い線のところで矢印のほうに折って重ねると、中の形はどうなるでしょうか。それぞれ右から選んで〇をつけてください。
- バナナのお部屋を見てください。今度は四つ折りにします。左の形を太い線のところで矢印のほうに2回折って重ねると、中の形はどうなるでしょうか。それぞれ右から選んで〇をつけてください。
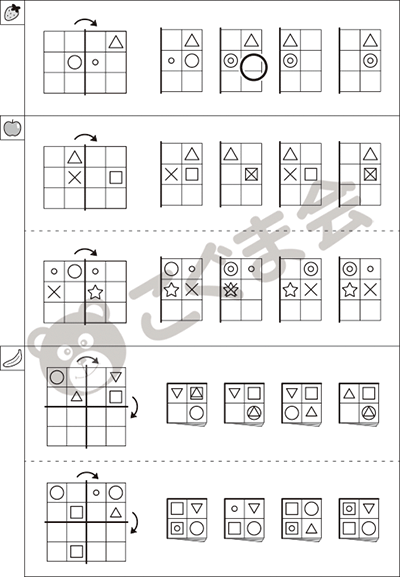
半分に折った時の重なり方を考える問題です。重ね図形の要素も入った応用問題ですが、一番下のバナナの問題は、一度左から右に折り、続けて上から下に折るという2回折りですのでやや難しくなります。このように、問題が複数ある場合、基礎的なものから応用的な問題に発展していくのが入試なのです。
- 同図形発見
-
- 左上のお部屋と同じ形で、赤いところが黄色くなっているものはどれですか。まわりから選んで〇をつけてください。
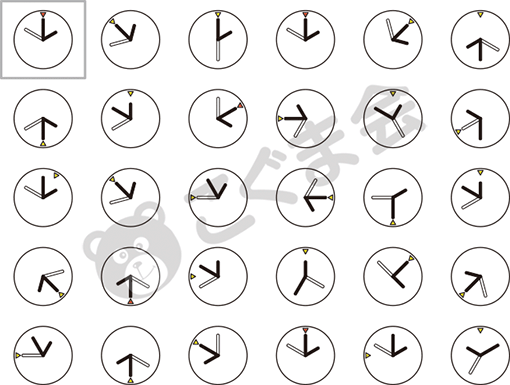
左上のお手本と同じ形を探す問題ですが、小さな△の色がお手本と同じ赤ではなく黄色のものを探さなくてはなりません。△がある場所、その色、3本の線の色・開き具合などいろいろな要素を見て判断する問題ですので、易しく見えてかなり時間のかかる問題です。制限時間が短いと相当難しい問題になります。
- 回転図形
- 上の形が下のように回るとどうなりますか。★の位置をよく見て、点を線でつないでかいてください。
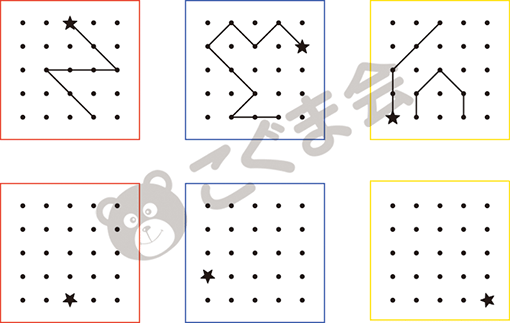
点図形の問題ですが、お手本が回転した場合どうなるかを考えて描かなくてはなりません。星印の位置がどう回転したかを考え、右に1回または2回、左に1回回転した場合の位置関係をイメージできるかどうかが問われます。やさしいようでかなり難しい問題の一つです。
- 折り紙の折れ線
- おり紙を長四角に2回折ると、どんな線ができますか。○をつけてください。
*実際の試験では、おり紙を折る様子が映像で流れました。
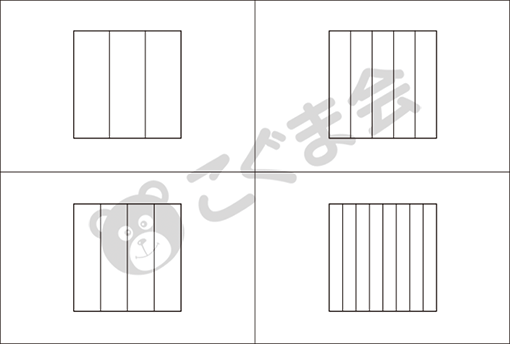
- おり紙を三角に3回折ると、どんな線ができますか。○をつけてください。
*実際の試験では、おり紙を折る様子が映像で流れました。
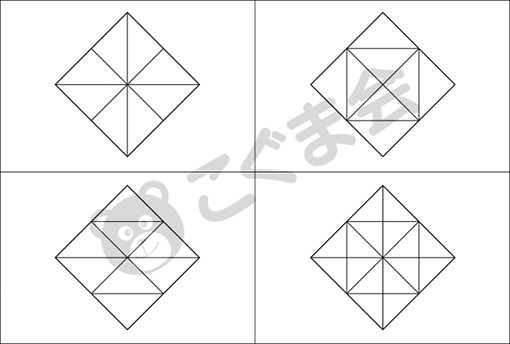
折り紙を使った課題は、線対称の問題(切って広げたらどんな形ができるか)が多いのですが、今回は長四角に2回折ったり、三角に3回折ったりした時にできる線を選択肢から選ぶ問題です。ほかにも折り紙を使った課題には、折って切った時何片に分かれるかを問う問題もあります。子どもたちが普段行う、折り紙を折ったり切ったりする経験をもとに問題が作成されていることに注目してください。
以上、今年の入試で出された図形課題のいくつかを紹介しました。まだ聞き取りが十分できていない学校もあるため不十分な点も多いと思いますが、全体の傾向としては、数の問題よりも図形の問題のほうが工夫された問題がたくさん出されているように思います。図形に苦手意識を持つ子が多くみられますが、身近にあるいろいろな素材を使って楽しく図形学習ができるように工夫してください。
- 読み・書き・計算はまだ早い!
こぐま会代表 久野泰可 著「子どもが賢くなる75の方法」(幻冬舎)
 家庭でできる教育法を一挙公開
家庭でできる教育法を一挙公開
子どもを机に向かわせる前に実際の物に触れ、考えることで差がつく。- 食事の支度を手伝いながら「数」を学ぶ
- 飲みかけのジュースから「量」を学ぶ
- 折り紙で遊びながら「図形」を学ぶ
- 読み聞かせや対話から「言語」を学ぶ

KUNOメソッド こどもがかしこくなる絵カード(幻冬舎)
幼児の日常生活の中にある学びをカード化!
おうちで体験できるKUNOメソッド子どもたちの生活の中でできる学習経験を、ご家庭でより実践しやすいようにカード化いたしました。お求めは、SHOPこぐま・こぐま会ネットショップ ・全国の書店・各書籍ECサイトにて