夏季講習会の授業から見えてきた子どもの学力の課題

第933号　2025年8月12日(火)
こぐま会代表　久野泰可

　夏休みを使って行う5日間の「総合力完成講座」の指導を通して、子どもたちが今も抱えている課題が見えてきました。朝10時から午後2時まで4時間連続の講座ですが、午前中は学力対策、お昼を挟んだ午後は劇づくりを通して行動観察対策をするという内容です。私が担当した学力対策は、初めに具体物を使った基本学習、そのあと6枚のペーパー課題を行うというものです。ペーパーだけで学習してきた外部生は、ペーパー課題はよくできていましたが、具体物を使った学習では作業に手が出せず、答えの根拠を求めても何も説明できない状況が目立ちました。正解できているのに、答えの根拠を説明できない子が多いのはなぜでしょう。解き方だけを教え込まれ、自分で考えて答えを出していない子の典型です。何が問題か具体的にお伝えします。

1.折り紙を使った線対称

(1)	指定された形を4つ折の真四角や三角から切り抜く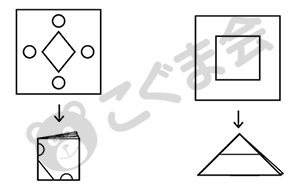

(2)	折り紙を開いた時、指定と同じ折り線がつくように折る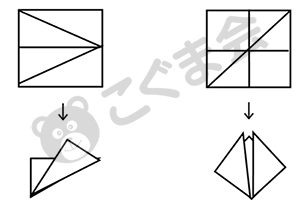

(3)	折り紙を折って切った時、何片に分かれるかを考える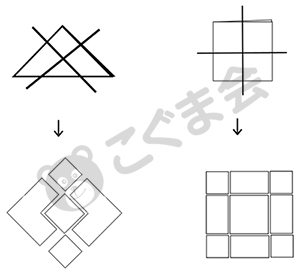

折り紙を使って行った3つの課題は、入試で出されたものでもあります。最初の問題は、線対称の課題としてよくやる内容ですが、次の折り紙を折った時の線のつき方を問う問題や、切った際に何片に分かれるかを問う問題は、日常的な課題でありながら、間違いやすい課題でもあります。ペーパーでやればできる課題でも、実際に折り紙でやるとできないのはなぜでしょうか。それは、解き方を身につけて機械的にやってできてしまうペーパー問題だけの練習では、本当に分かったことにならないということなのです。(2)も(3)も実際の経験が生きてきます。

2.魔法の箱

(1)	箱の中でどんな変化が行われるかを判断し、色・向き・数の変化等の法則性を発見する

(2)	数の変化について、きめられた法則を当てはめ、最後にどんな数になるか考える＊入試問題を使った練習を基本とします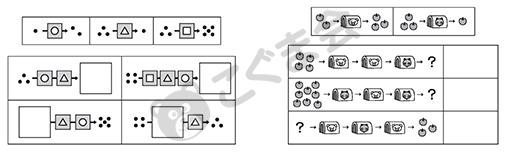

魔法の箱の変化は、必ずしも数の変化だけではありません。その変化の意味を捉えられるかどうかがポイントです。魔法の箱に関する問題には、3つのタイプがあります。数の変化で見ると、

a.
最後にいくつになって出てくるかを考える: b.
最後に出てきた数を見て最初に入れた数を求める: c.
数の変化を見て、どんな魔法の箱を通ったかを考える

この中で難しいのは、b.の逆思考のタイプの問題です。元に戻る発想はほかでも求められますが、数の変化における逆思考は子どもたちにとってはかなり難しい課題です。一つずつ戻らなくてはなりませんから、集中力が求められます。

3.つみ木の変化・移動

(1)	立方体つみ木８個で見本と同じ形を作り、それを１個ずつ移動した見本を見て、どれを移動したか考えて構成する
(2)	はじめの形から何個か変化した積み木を見て、何個動かしたか考える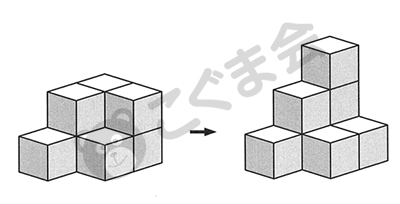

(1)は、８個のつみ木を１個ずつ動かして形を変えていく課題です。１個ずつ動かしながら最後に元の形に戻ってくるので、「つみ木の山手線ゲーム」と命名して行っていますが、子どもたちも楽しんで取り組んでいます。三角パズル８枚でも行いますが、ポイントは、何が変わって何が変わっていないかを素早く観察することができるかどうかです。１つ動かしただけでも全体の形のイメージが大きく変わることがありますので、その変化の中で何が動いたのかを見抜く力が大事です。

右のつみ木をいくつか動かして、矢印の左の形にしました。動かした数だけ下のお部屋に〇をかいてください。

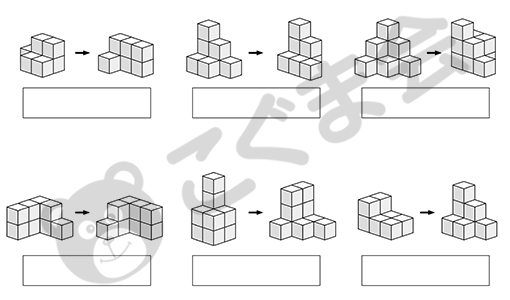
この経験を踏まえ、今度は積まれた２つのつみ木を見て、何個動かせばいいのかを考える(2)の課題に取り組みました。もちろん最小の数だけ動かすという前提での課題ですが、１個だけならまだしも、２個、３個となると相当形も変わりますので難しい内容になります。変化するものと変化しないものをしっかり区別して観察できるかどうかは、いろいろな場面で求められる大事な能力です。

4.置き換えの応用問題

動物村の果物屋さんは次のように果物を取り替えてくれます

ミカン１個はクリ２個と交換できる
ブドウ１房はミカン２個と交換できる
リンゴ１個はミカン１個とクリ１個と交換できる

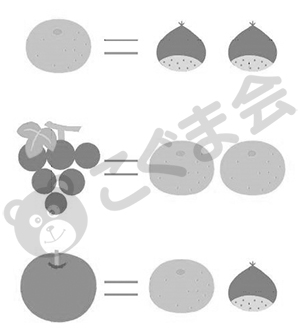
問題例

(1)	クリ４個はミカン何個と交換できるか
(2)	ブドウ２房は、クリ何個と交換できるか
(3)	リンゴ４個は、ブドウ何房と交換できるか

一対多対応の考え方を応用した課題です。今回の約束に即していえば、

１
ミカンからクリを聞いたり、ブドウからミカンを聞く課題はかけ算の考え方: ２
クリからミカンを聞いたり、ミカンからブドウを聞く課題は包含除の考え方

で、この２つはほとんどの子が正解できています。ただし次の問題になるとまだ正解できない子が多く見られます。

１
ブドウ２房はクリ何個と交換できますか: ２
リンゴ４個はブドウ何房と交換できますか

ミカンを仲立ちにしてブドウとクリの関係を考えたり、ミカンとクリを仲立ちにしてリンゴとブドウの関係を考える問題は、かなり思考力が要求されます。
子どもたちは、果物のシールを貼ったおはじきを操作しながら、答えを導き出していましたが、こうした試行錯誤が大事なのです。ペーパーだけの学習ではこうした試行錯誤の時間がないため、自分の答えのプロセスを言語化できないのです。これでは応用力は身につきません。本当に理解したということはどういうことか、今一度考えてみてください。こう見てくると、ペーパー主義の受験対策は、子どもたちの考えるチャンスを奪い、主体的な学びの育成を奪ってしまっていると言わざるを得ません。

さて、その後、毎日6枚のペーパーを使って、答えの根拠を発表する授業を中心に進めました。ペーパーの難易度は、入試問題レベルですのでかなり難しい内容です。全体で36枚のペーパーの中から、まだ壁になっている課題がいくつかあることがわかりました。それは次の７つの課題です。

1	数の総合問題：生活場面を見て四則演算の操作を行う課題
2	四方からの観察と鏡映像の複合問題：鏡への映り方と反対側から見た時の見え方の違い
3	しりとり：逆しりとり
4	飛び石移動：移動する２つのものがどこで追いつき、どこで出会うか
5	シーソーにおける消去の考え方：両方に同じものが載っているとき、同じものを降ろして考えることができる
6	交換：仲立ちを伴う交換
7	重ね図形：半分に折って重なる場合にどんな図形ができるか

この７つの課題は、入試でもよく出される課題ですので、基礎をしっかり身につけ、そのうえで少し背伸びさせながら挑戦させてください。難しい課題に挑戦させながらいつも感じることは、基礎がしっかり身についているかどうかが〇×の分かれ目になるということです。逆に言えば、基本がしっかり身についていない状態で、いくら難しい過去問をやっても理解できないし、身につかないということです。背伸びしすぎでは、教育効果が見られないのです。

こぐま会代表　久野泰可監修　2025年度小学校入試厳選50問 - 傾向をつかんで、一歩前へ: 全問に詳しい解説付き。最新入試問題から到達目標や対策方法を正確に知り、確実な対策を！
　
※「ショップこぐま」で購入された方には、冊子「2025年度小学校入試分析速報」を進呈いたします。（非売品・部数限定）

次のコラム
目次
前のコラム