ページ内を移動するためのリンクです
MENU
ここから本文です
週刊こぐま通信
「代表のコラム」

がんばれ受験生 (4)
なぜ「逆思考」の問題が多いのか

第908号　2024年10月11日(金)
こぐま会代表　 久野 泰可

今年行われた小学6年生の算数学力テストの最初の問題は次のようなものでした。
ゆうまさんたちは、折り紙で遊んでいます。 ゆうまさんは、折り紙を72枚持っています。ゆうまさんが持っている折り紙は、こはるさんが持っている折り紙より28枚少ないです。こはるさんが持っている折り紙の枚数を求める式を、下の ア から エ までの中から1つ選んで、その記号を書きましょう。

　ア　72＋28
　イ　72－28
　ウ　72×28
　エ　72÷28

えっ、これが６年生の問題？ 数字を小さくすれば幼児でもできそうな問題がなぜ６年生に？と思うのは私だけでしょうか。 しかし、よくよく考えてみれば、関係性を考える算数的な思考を見る意味ではとても良い問題だと思います。2人が持っている折り紙の数を比較する話ですが、ゆうまさんから見た場合の数量関係を、もう一方の当事者であるこはるさんから見た場合どうなるのかを問いかけています。この問題を私が今担当している２年生にやってもらったところ、正解できたのは半分以下でした。間違った子の多くが（イ）の７２－２８を選んでしまったのです。たぶん「少ない」という言葉に引きずられて、７２－２８を選んだのではないかと思います。2人が持っている折り紙を比較した時、多いほうから見た場合と少ないほうから見た場合の関係性を事実に即してイメージできるかどうかが問われています。書かれている数字や言葉だけを頼りに式を考え、二者の関係性をイメージできない子が多いのではないかと思います。
私がなぜこの問題を紹介したかというと、最近の小学校の入試問題を見ると「逆思考」の問題が多く出され、それが今回のこの問題と大いに関係があると考えているからです。 そもそも論理的思考力とは何なのでしょうか。私は、ピアジェの認識論をベースにメソッドを構築してきました。すなわち、幼児期の子どもたちは思考において自己中心的であり、一つの観点にこだわるとほかの観点が見えてこないということを、水量保存の実験を通して説明しました。
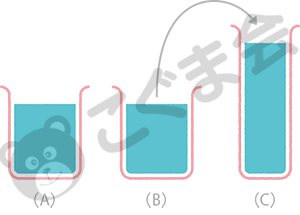この量の保存の問題は、視点を変えて物を見ることができるかどうかが問われる典型的な問題です。年中ごろまでは、背の高いほうが多いと答える子が多くみられます。「なぜ？」と聞くと「だって背が高いから」と背の高さで量を判断します。しかし年中を過ぎると自信をもって「同じ」と言えるようになります。「なぜ？」と聞くと、「だって移し替えるときにこぼさなかったから」とか「背が高いけど、細くなっているだけだから同じ」と、別な観点に気づきます。そのうえ、元に戻せばきっと同じになるに違いないと予測します。つまり、背の高さだけで量を判断していた子どもが、ほかの観点に気づき「同じ」と正解できるのです。
このように、論理数学的思考を育てるためには、視点を変えて物事を見る眼を育てることが大事です。こぐま会の教育は、「考える力」を育てる教育として、この「視点を変えて物事を見る」経験をあらゆる場面で大事にしています。小学校入試が難問化していく背景には、この思考が求められているのです では実際の問題を見てみましょう。

1. 四方からの観察
動物たちがテーブルの上のつみ木を見ています。
  • それぞれの動物たちから、つみ木はどう見えますか。右のお部屋から選んで動物と線結びしてください。

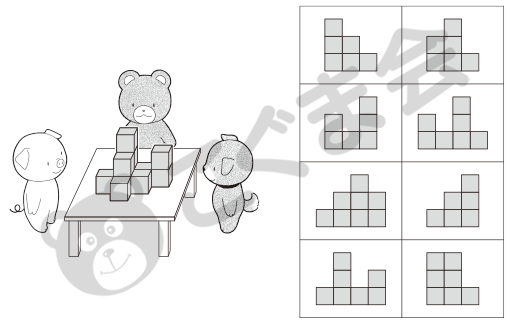
つみ木の見え方をその場に行かないで判断する問題です。自分からの見え方を離れて、違う場所からの見え方をイメージできるかどうか。ピアジェの思考実験でも取り上げられた問題です。

2. しりとりにおける逆思考（逆しりとり）
左上のお部屋を見てください。ブタ→タヌキ→キツネと、しりとりでつながりますね。では逆さしりとりで「キツネ」から考えます。「キツネ」の「き」が「タヌキ」の「き」とつながって「タヌキ」の「た」が「ブタ」の「た」とつながります。
  • 逆さしりとりで青い★のお部屋の「ラッパ」が最後になるように、青でつないでください。ラッパを入れて３つの絵がつながります。
  • 逆さしりとりで赤い★のお部屋の「かさ」が最後になるように、赤でつないでください。かさを入れて３つの絵がつながります。

しりとりは、最初の言葉の最後の音を次の言葉の頭に持ってきて繋げていく言葉遊びです。遊びとしても行われているものですから、後ろにつなげていくことは容易にできます。しかし「逆しりとり」は、終わりの言葉から一つずつ前に戻って最初の言葉までつなげるものです。しりとりのルールを逆から考える問題です。

3. 魔法の箱における逆思考（出てくる数ではなく、入れた数を考える）
上のお部屋を見てください。白い〇がイヌの箱を通ると数が１つ増えます。ネコの箱を通ると２つ増えます。クマの箱を通ると半分になります。
  • 上のお約束で下のように箱を通ったとき「？」のところにはどんな数や動物が入りますか。上２つのお部屋は「？」に入る数だけ右に〇をかいて、下のお部屋は「？」に入る動物を右から選んで〇をつけてください。

「魔法の箱」と呼んでいる課題は、ある約束で数が変化する箱を通過するとき、最後にいくつになって出てくるかを考える問題です。変化の法則性を発見する問題ですが、出てくる数をみて入れた数を考える問題が、魔法の箱における逆思考の問題です。最近この問題が多くの学校で出題されています。

4. 数の操作における逆思考（途中の数が抜け、最後から戻ってその数を考える）
  • 太郎さんは魚釣りに行って５匹釣りました。一緒に行った次郎君から何匹かをもらったので、太郎君のお魚は9匹になりました。何匹次郎君からもらったのでしょうか。
  • バスにお客さんが何人か乗っていました。次の停留所で4人降りて6人乗ってきたので、お客さんは12人になりました。何人乗っていたのでしょうか。

数の変化において、途中の数が抜けてしまい最後の数から戻って考える「逆思考」の問題です。小学校1年後半から2年にかけて、□を使って式を立てる練習をしますが、幼児はこれを暗算で解かなければなりません。話を聞いて場面がイメージできるかどうかが問われます。

冒頭で紹介した、学力テストの2問目は以下のような問題でした。

たくみさんは、はじめに折り紙を何枚か持っていました。 ゆうまさんから38枚もらって、全部で62枚になりました。このことを、たくみさんがはじめに持っていた折り紙の枚数を□枚として式に表します。下の ア から エ までの中から、正しい式を1つ選んで、その記号を書きましょう。

　ア　62＋38＝□
　イ　□ ＋38＝62
　ウ　□－62＝38
　エ　□－38＝62

小学校入試では、ほかにもいろいろな形で「逆思考」が求められています。そのことが小学校の入試問題を難しくしていますし、学校側は、そのことを通して「考える力」を見ようとしています。受験生の皆さん、この「逆思考」の問題をもう一度おさらいして、入試に臨んでください。


読み・書き・計算はまだ早い！

 こぐま会代表 久野泰可 著「子どもが賢くなる75の方法」（幻冬舎）

 家庭でできる教育法を一挙公開
子どもを机に向かわせる前に実際の物に触れ、考えることで差がつく。
  • 食事の支度を手伝いながら「数」を学ぶ
  • 飲みかけのジュースから「量」を学ぶ
  • 折り紙で遊びながら「図形」を学ぶ
  • 読み聞かせや対話から「言語」を学ぶ

 KUNOメソッド　こどもがかしこくなる絵カード（幻冬舎）

 幼児の日常生活の中にある学びをカード化！
おうちで体験できるKUNOメソッド
子どもたちの生活の中でできる学習経験を、ご家庭でより実践しやすいようにカード化いたしました。
お求めは、SHOPこぐま・こぐま会ネットショップ ・全国の書店・各書籍ECサイトにて

PAGE TOP