第5回教育セミナー「考える力を育てる学習法」

第549号　2016年10月7日(金)
こぐま会代表　久野泰可

　来年以降の受験を目指す保護者の方々を対象に、6月から行ってきました「合格のための室長教育講演会」の第5回目を、10月2日午前に行いました。今回は、「考える力を育てる学習法」というテーマで、受験を含め、幼児期の基礎教育の進め方について具体的にお伝えしました。講演会の内容は以下の通りです。

第5回合格のための室長教育講演会「考える力を育てる学習法」: 1. 入試で求められる「考える力」とは

入試問題を使って、求められている「考える力」を分析する

2. 保存問題に見られる幼児期の思考の特徴

幼児のものの見方・・・知的自己中心性（ピアジェ）
いかに脱中心化するかが教育の課題・・・可逆的思考を可能にするために
第1回ステップ別発達診断テストの解答例

3. なぜ事物教育が大切か

「アクティブ・ラーニング」がなぜ必要か
幼児期の基礎教育は、事物教育しかありえない

4. 領域の学習を貫く思考の基本

最初に、最近の入試問題の中で、「考える力」が求められる16の課題を示し、そこで求められる考え方、また子どもがつまづく原因を一つ一つ明らかにし、単なるトレーニングで解決する問題でないことを強調しました。次の問題はその典型です。

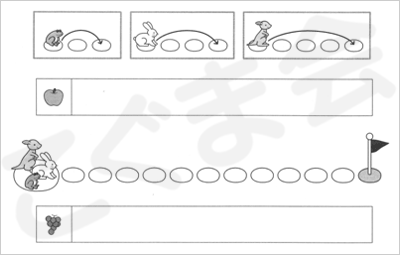
「飛び石移動」

カエルとウサギとカンガルーが飛び石を跳んでいきます。3匹は一緒に跳びますが、カエルは1つとばし、ウサギは2つとばし、カンガルーは3つとばしで進みます。

【問題】

3匹がそれぞれ2回ずつ跳んだとき、カエルとカンガルーの間に飛び石はいくつありますか。リンゴのお部屋にをかいてください。
真ん中の飛び石の絵を見てください。カンガルーがゴールに着いたとき、カエルとウサギはどこにいますか。カエルのいる場所に、ウサギのいる場所に×をつけてください。
カンガルーはゴールまで行ったら、今度は折り返して戻ってきます。カンガルーとカエルが一緒に跳び始めると、戻ってきたカンガルーがカエルに会うのは、はじめから数えると何回跳んだときですか。その数だけブドウのお部屋にをかいてください。

ここで求められる「思考力」をどういう手順で育てるのか。そのためには、どうしても物事に働きかける経験が必要であることをお伝えしました。この問題の場合、まず約束通りに動くことができるかどうかがポイントで、その上、最後の「カンガルーとカエルが一緒に跳び始めると、戻ってきたカンガルーがカエルに会うのは、はじめから数えると何回跳んだときですか？」の問題は、旅人算の幼児版ともいえる問題です。作業して答えを導き出すこうした問題が、最近の入試問題の傾向と言えます。

ところで、心理学者のピアジェが、子どもの思考がどのように育つのかを説明した有名な実験があります。量の保存の実験ですが、今回はこれを用いて子どもの思考の特徴をお話ししました。

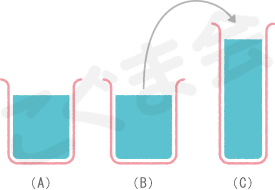
「量の移し替え」: 同じ大きさのコップ（A）と（B）に、同じ量の水が入っています。このうち、（B）の水を細長い（C）のコップに移し替えました。（A）のコップと（C）のコップでは、どちらがたくさん水を飲むことができますか？

年中の1月に行ったテストでは、正解者は全体で30パーセントくらいでした。不正解者の大半は、背の高くなった(C)のほうが多いと答えます。その理由の多くは、「背が高いから」です。しかし、月齢が進むにつれ、「同じ」と言えるようになってきます。別な視点に気付き始めたからです。すなわち、「背は高くなっているけど、容器は細くなった。」「移す時こぼしはしなかった。」「元に戻せばきっと同じになるに違いない」・・・こんな理由で、「同じ」と答えられるようになります。この問題を繰り返しトレーニングした結果ではなく、自ら考えて正解を導き出しています。今まで、ひとつの視点でしか物事を判断できなかった子どもたちが、さまざまな経験・学習を通して視点をたくさん持てるようになった結果、正解に至るのです。

背の高さだけで判断していた子どもたちが、違う視点に気づき始め、その結果「同じ」と言えるようになっていくのです。このように、たくさんの視点を持つことができるようになるのが幼児期の教育課題であるし、このことは、相手の立場に立って気持ちを考えるという社会性の発達にも関係がありそうです。こうした「考える力」を育成するには、最初からペーパーを使って知識を教え込む方法ではなく、物事に働きかけ、試行錯誤しながら結論を導き出す経験が必要です。それは「事物教育」によってしか実現できません。アクティブ・ラーニングがはやりの昨今ですが、幼児期の基礎教育は、事物教育を置いて他に方法はありません。
今回は、それぞれの領域で難しいとされる入試問題をいくつか分析してお伝えしましたが、もう一つ大事な観点があります。それは、領域を越えて学校側が入試で求める「考える力」は何かということです。これを抑えておかないと、多様化した問題、工夫されたオリジナルな問題に対応できません。それを皆さまにご紹介しました。

領域を越えて学校側が求めている考える力とは

ものごとの特徴をつかむ
同図形発見・何が変化したかを捉える・私は誰でしょう
いくつかのものごとを比較する
一対一対応・量の系列化・シーソー
ある観点に沿って、物事を順序づける
量の系列化・位置の系列化・時系列
全体と部分の関係を把握する
数の構成・図形構成
観点を変えてものごとを捉える
四方からの観察・地図上の移動・数のやりとり
物事を相対化してとらえる
量の相対化・シーソー・関係推理
逆に考える
逆思考・逆対応
あるものごとを、ひとまとまりにして捉える
一対多対応・包含除
規則性を発見する
法則性の理解・魔法の箱・観覧車
AとB, BとCの関係からAとCの関係を推理する
シーソーのつりあい・交換

最後に、最近ばらクラス（年長児）の「数のまとめの授業」で行った問題を紹介し、解くためにどんな力が必要かを一緒に考えました。工夫された問題が多く出題されている最近の入試問題を分析していくと、小学校高学年で学ぶ「特殊算」につながる問題が出され始めています。

「消去の考え方」

上のお部屋を見てください。
動物村の果物屋さんに、ウサギとクマが買物に来ました。ウサギはリンゴ2個とミカン1個を買って、ドングリ5個を払いました。クマはリンゴ2個とミカン2個を買って、ドングリ6個を払いました。
クマの方がドングリを1個多く払っていますね。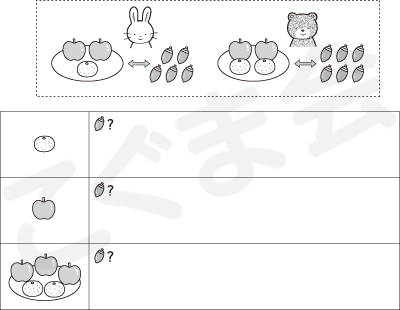

【問題】

ミカン1個の値段は、ドングリいくつでしょうか。その数だけミカンのお部屋に青いをかいてください。
リンゴ1個の値段は、ドングリいくつでしょうか。その数だけリンゴのお部屋に青いをかいてください。
リンゴ3個とみかん2個の値段は、ドングリいくつでしょうか。その数だけ1番下のお部屋に青いをかいてください。

ウサギとクマが買ったリンゴとミカンの数の違いと、払ったドングリの数を見て、リンゴ1個とミカン1個の値段（ドングリの数）を求める問題で、典型的な消去算の考え方が求められます。この問題を作った際、2人の買ったものや払ったものを見ただけでは多分幼児には難しいだろうと考え、設問の最後に「クマのほうがドングリを1個多く払っていますね」というヒントのようなものを入れました。その上でやってもらいましたが、予想した通り、ミカン1個がドングリ1個と最初から答えられた子は、クラスの半分くらいしかいませんでした。このミカン1個が分からないと下の2問も答えられませんから、そこでいったん答え合わせをし、ミカン1個がドングリ1個だということを踏まえて下の2問をやってもらうと、7割の子が理解できていました。

この問題の場合、最後に「クマさんのほうが1個多く払ったね」と言われなくてもできる子は、相当考える力が身についていると思います。ポイントは、両者を比較し、同じところと違うところを発見し、そこから「なぜ、クマさんのほうが1個多く払ったのだろう？」「そうか、ミカンを1個多く買っているからだ」「だから、ミカンの値段はドングリ1個」と導きだせるはずです。「違い」の意味を考えてみることができるかどうかがポイントです。また、ミカン1個がドングリ1個と分かってから、どのようにしてリンゴの値段を導き出したのか、子どもに尋ねると「だってウサギさんが買ったミカンはドングリ1個だし、そうすると、リンゴ2個でドングリ4個になるから、リンゴ1個はドングリ2個」とちゃんと説明できるのです。これには、私も驚きました。感覚で答えが導き出せないわけではありませんが、きちんと論理的に説明し答えられる年長児を見ると、まだまだ高度な問題にチャレンジできる可能性はあるな・・・と内心うれしくもなりました。

保存の問題に象徴されるように、徹底してトレーニングして答えを教えるのではなく、それまでに身に付けたいろいろなものの考え方が総合されて、ひとつの問題の解決につながるようにしなければなりません。保存の問題は、答えを教えてしまえば単純な問題ですが、「なぜ？」に自らの言葉で答えられるようにしなければ、本当の意味で分かったことにはなりません。か×かで即断するのではなく、限りなくに近い×もあるし、限りなく×に近いもあるということを指導者は知っておかなければなりません。その上で、次に何を学ばせるか・・・そこで指導者としての力量が問われていくのだと思います。