週刊こぐま通信
「室長のコラム」「考える力を求める入試問題(5) 図形領域の課題」
第714号 2020年3月20日(金)
こぐま会代表 久野 泰可
こぐま会代表 久野 泰可

小学校入試における図形領域の課題は、数・言語と同じように重要な柱になっています。最近は数領域の出題が減る一方で、図形領域の問題は増えているように思います。なぜでしょう。その理由のひとつに、その学校独自の問題が作りやすいという面があるように思います。数の領域は将来の四則演算につながる内容がほとんどで、どうしてもパターン化しやすい面を持っています。それに比べ、図形領域は同じ趣旨の問題でもいろいろ工夫ができ、他校と違った問題が作りやすいという面があるように思います。知能検査の問題が入試問題の中心であった40年近く前の入試では、「同図形発見」「点図形」「図形模写」のように決まったテーマが多く、問題の意図を伝えなくても、子ども自身がペーパー問題を見れば何をすべきか分かる問題がほとんどでした。今もこのテーマがなくなったわけではありませんが、考える力を求める良い問題がたくさん出されるようになりました。
こぐま会の基礎教育では、入試に出る - 出ないに関係なく次のような課題を学習し、その発展の上で入試問題に取り組んでいます。
- step1「基本図形とその構成」
- step2「立体構成」
- step3「同図形発見、点図形」
- step4「図形分割」
- step5「展開図、線対称」
- step6「重ね図形、回転図形」
- 1. 図形構成
- 左の形を組み合わせてできる形を右から選んでをつけてください。

- 2. 図形構成
- 左のお部屋の形を合わせるとどんな形ができますか。右の4つの中から選んでをつけてください。
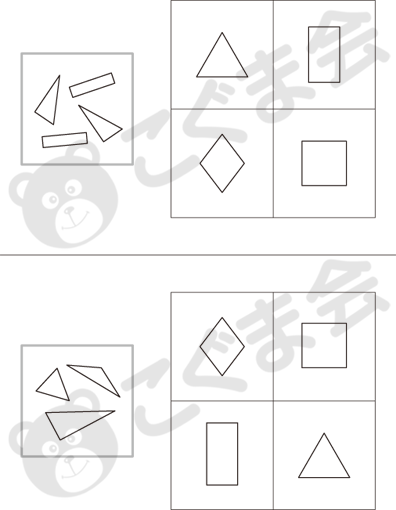
1.も 2.も特に目新しい出題ではありませんが、2.のほうがやや難しいようで間違いも目立ちます。どのように構成するか、実際のパズル等を構成する経験が意味を持ってくる問題です。
「図形構成」「図形分割」が出題の中心であった時代から、現在は少し変化して「対称図形」「重ね図形」「回転図形」などの新しい課題が出始めているのが特徴です。今回はその中でも重ね図形と回転図形についてご紹介しましょう。
- 3. 形の重なり(聞き取り)
- 星と雲だけが重なっているところにをつけてください。
- 3つとも全部重なっているところに×をつけてください。

- 4. 重ね図形
- この形は透明な紙にかいてあると考えてください。左の2つの形をそのまま重ねるとどうなりますか。右から選んでにをかいてください。
- 5. 重ね図形
- 左のお部屋を見てください。左の形を真ん中の線で矢印のほうに折って重ねると、右のようになりますね。
同じように真ん中の線で矢印のほうに折って重ねたとき、どのようになりますか。それぞれ右から選んでをつけてください。
- 左のお部屋を見てください。左の形を真ん中の線で矢印のほうに折って重ねると、右のようになりますね。
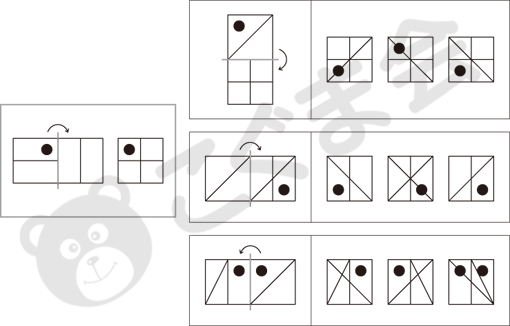
重ね図形の始まりは、集団用の知能テストの問題です。それは、今回の3.のようにいくつかのもの(野菜・果物・動物など)が重なり合っていて、一体何が重なっているかを考える問題でした。3.は月と星と雲が重なっているもので、星と雲だけが重なっているところ、3つとも全部重なっているところというように、どこでどう重なっているかを考える問題です。最近の問題の多くは、4. 5.のように図形を使った重ね図形が多く、4.はそのまま上に重ねたときにできる模様を探し、5.は半分に折って重ねたときにできる模様を探す課題です。このように、図形の重なりには2つの重ね方があり、そのままずらして上に重ねる場合と、半分に折って重ねる場合とをしっかり区別して理解しなければなりません。重ね図形が難しいのは、この2つの方法があるということと、特に半分折りの重ね方が難しいという点があり、結果として子どもたちにとって苦手意識を持ちやすい問題になってしまうのです。5.のような問題をぜひ繰り返し練習してください。
図形課題の中でもうひとつ触れておかなければならない問題があります。それは「回転図形」です。もともと回転推理といわれる課題は「観覧車」に象徴される内容ですが、図形を使った回転推理、つまり「回転図形」の課題も増えています。ある形が右や左に回転したとき図形の位置関係がどうなるかを考える問題ですが、頭の中で回転のイメージを持つのはとても難しい課題です。最近いろいろ出題されていますが、2020年度入試では以下のような問題が出ています。
- 6. 回転図形
- 上の赤いのお手本が回転して、下の青いの向きになると、中の線はどうなりますか。線をかいてください。
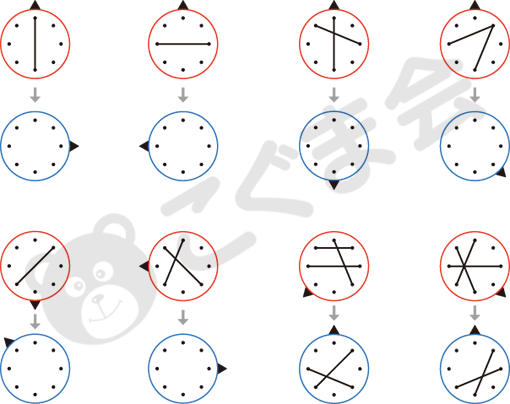
この問題は「位置の移動」とも考えられますが、突起した部分の位置が変わることによって時計の針のような線がどうなるかを考える問題ですから、全体を図形的に捉えれば図形の回転と考えることができます。ただ、8個の点の位置に注目して、その位置が突起した部分との兼ね合いでいくつ動いたかを考えれば、観覧車で問われる問題と同じようになり、広い意味で「回転推理」とした方がいいかもしれません。 この他にもいろいろ工夫された問題がありますが、変化に対する敏感さが要求され、「考える力」が問われる次のような問題が今後も増えていくと予想されます。
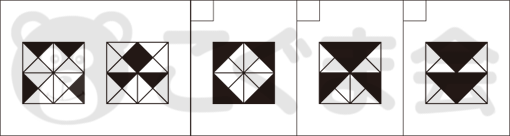
- 7. つみ木の変化
- 左のお部屋を見てください。上の色がついた2つのつみ木を横に1つずらすと、つみ木はどうなりますか。下から選んでをつけてください。
- 真ん中のお部屋を見てください。上の形から色のついたつみ木1つを動かすと、どんな形ができますか。下から選んでをつけてください。
- 右のお部屋を見てください。今度も上の形から1つ動かして下の形を作りました。動かしたのはどのつみ木でしょうか。上の形の動いたと思うつみ木に色を塗ってください。
