週刊こぐま通信
「室長のコラム」「考える力を求める入試問題(3) 数の課題」
第712号 2020年3月6日(金)
こぐま会代表 久野 泰可
こぐま会代表 久野 泰可

今回は2020年度入試問題の中から「数」に関する問題を紹介し、どんな考え方が求められているかをお伝えしたいと思います。最近の入試では、数の問題が占める割合が小さくなっているように思います。昔から数・図形・言語が入試問題の中心であることは間違いありませんが、その中でも一番多く出されていた数の問題が減少しています。なぜなのでしょうか。
- 数の問題はパターン化しやすく、学校独自の問題を作るのにあまり向いていない
- 機械的なトレーニングでできてしまう問題が多く、思考力を問う問題は図形のほうが作りやすい
- これまで別々に出されていた四則演算のもとになる問題が、「数の総合問題」として一括して出されるようになり、例えばこれまで3枚のペーパーで行っていた問題が1枚で済むようになったため、問題数がより少なくなったように感じる
こうした全体の状況の中で、どんな数の問題が出されているか、紹介しましょう。
- 1. 分類計数
- 左上の赤いのお部屋を見てください。が3つかいてありますね。これは真中のお部屋にある赤いの数と同じです。
- 同じように、それぞれいくつあるか数えて、その数だけ周りにあるその絵のお部屋にピンクのをかいてください。似ている形がありますから、注意してやってください。
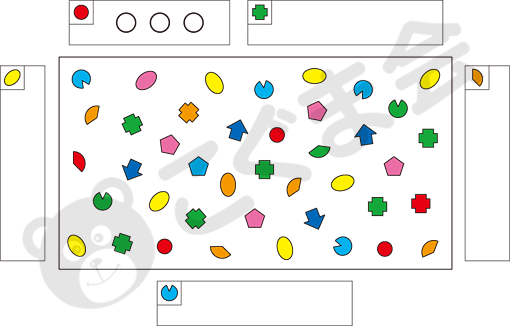
これは、昔からある典型的な問題で、正確に数えることができるかどうかということです。数え忘れがあったり、二重に数えたりしないように、しっかり作業して答えを導き出す必要があります。難しい問題だけでなく、こうした基本問題は今でも数多く出されています。
- 2. 数の増減
- よし子さんの家にミカンがたくさんありました。よし子さんはだいすけ君にミカンを4個あげたあと、自分で2個食べました。食べたらこれだけ残りました。ミカンは最初にいくつあったでしょうか。その数だけ下のお部屋にをかいてください。
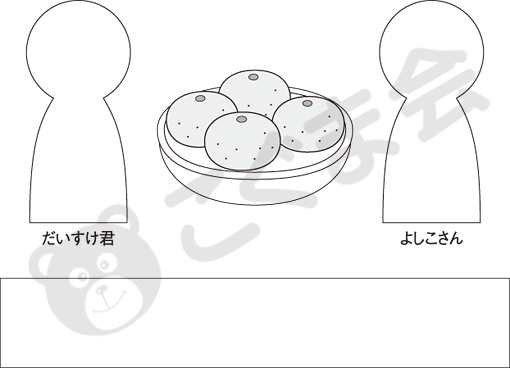
数の変化(増減)を考える問題ですが、最後の数を答えるのではなく、最初の数を答える「逆思考」の形をとっています。-4-2=4 という話の、最初の数 を求める問題です。ひとつずつ前に戻ることが基本ですが、この場合、あげた数と自分で食べた数を最初に求め、-6=4と考えてもいいわけです。この逆思考の文章題は、小学校1年生の後半で学習するものですが、答えは出ても立式が難しい問題のひとつです。このあたりが出題の根拠になっているのではないかと思います。
- 3. 数の総合問題
- 遊園地で動物達が遊んでいます。
- コーヒーカップに乗っているウサギさんとクマさんでは、どちらが多いですか。右下のお部屋の多いほうにをつけてください。
- ジェットコースターは1つの台車に2匹ずつ乗ります。新聞を読んでいるクマさんは何番目の台車に乗りますか。クマさんの乗る台車に色を塗ってください。
- お化け屋敷の中に5匹います。また4匹入って、2匹出ると中のお客さんは何匹になりますか。その数だけバナナのお部屋にをかいてください。
- 3匹ずつ乗れる観覧車のカゴが2つあきます。並んで待っている動物が乗ると何匹残りますか。その数だけミカンのお部屋にをかいてください。
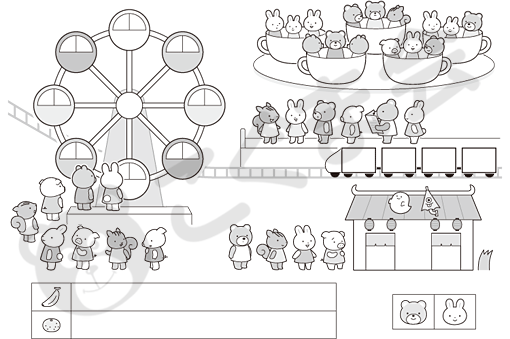
こうした、生活の一場面を使ってさまざまな数の問題を投げかけていく問題を、「一場面を使った数の総合問題」と呼んでいます。今回は遊園地の場面ですが、その中で、1.は「数の多少」、2.は「一対多対応」、3.は「数の増減」、4.は「一対多対応」の問題です。これまではいずれも別々のペーパーで出題されていたものですが、それが一場面の絵を使ってすべて問いかけることができる・・・こうした問題が現在の主流になっています。質問に答えるためにどこの数を見ればいいのかを自分で判断しないと、間違えてしまいます。その意味で観察力や作業能力も求められています。同じような問題は他校でも出されています。
- 4. 数の増減とやりとり
- クマ、イヌ、パンダが持っているりんごの半分の数を、同時に矢印の方にいる動物にあげます。2回、同時に矢印の方にいる動物にりんごをあげたとき、パンダが持っているりんごの数はいくつになりますか。下のお部屋にをつけてください。
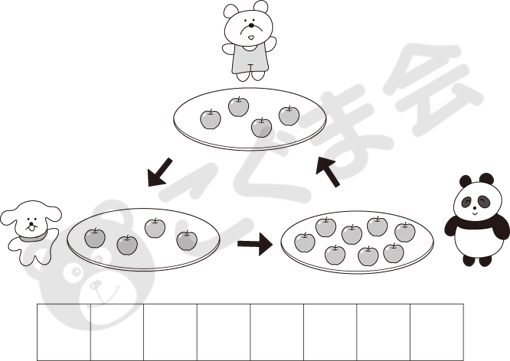
今回の入試における数の問題の中で「考える力を求める数の問題」として出色の出来といえるものは、多分この問題だろうと思います。きわめて生活的なありふれた場面の問題ですが、3者の間で半分の数を同時にあげる、そしてそれを2回繰り返すという設定が問題を難しくしています。1匹の動物がもらう役とあげる役を同時に行うという点に思考と作業がついていくか。大変工夫された問題だと思います。
この他に、他の領域と関連付けながら数の能力が求められる問題があります。それは「未測量におけるシーソーのつりあい」の問題です。今回も何校かで出されていますが、典型的な問題は以下の通りです。
- 5. つりあい
- 上のシーソーを見てください。
キャベツ1個はタマネギ3個とつりあっています。
タマネギ2個はナス4個とつりあっています。- キャベツ2個はタマネギ何個とつりあいますか。その数だけリンゴのお部屋にをかいてください。
- タマネギ4個はナス何個とつりあいますか。その数だけバナナのお部屋にをかいてください。
- キャベツ1個はナス何個とつりあいますか。その数だけブドウのお部屋にをかいてください。
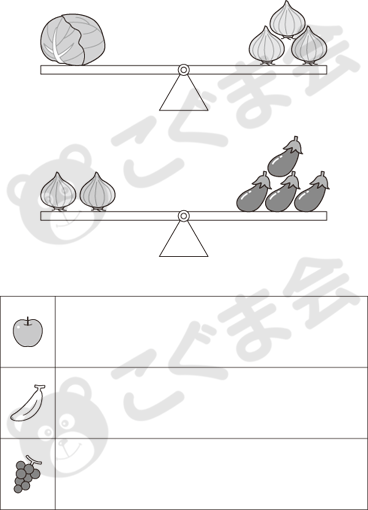
キャベツ(A) とタマネギ(B)、タマネギ(B) とナス(C) のつりあう条件を示し、その上で、3つの問題が出されています。最初は、A=3Bの関係を踏まえて、2A=Bを考える問題です。これは一対三対応と考えれば、特に難しいわけではありません。次に2B=4Cの関係を踏まえて4B=Cを考える問題ですが、これも受験生には特に問題なくできると思います。最後の1A=Cの問題は、置き換えを伴う交換となりかなり難しい問題です。AとCの関係をBを仲立ちとして考える問題です。この問題の背景にあるのは、かけ算の考え方(一対多対応)の課題です。シーソーのつりあいの問題は、こうした数の問題として捉えておく必要があります。この置き換えの問題は、逆からの問いかけもある関係で、将来のかけ算・わり算の基礎として重要です。この交換の問題は、数の問題の中で一番難しいといっても過言ではありません。
2020年度の数の出題は、総じて易しい問題であったように思います。しかし10年位さかのぼってみてみると、かなり難しい数の問題もたくさん出題されています。その項目を挙げると、
- 一対多対応
- 交換
- 数のやり取り
- 数の増減と一対多対応の複合問題
- step1「計数、同数発見、5の構成」
- ・買いものごっこ(命令行動)
・5の構成
・おはじきを数える
・カードを使った同数発見 - step2「一対一対応」
- ・対応に必然性のある一対一対応
・対応に必然性のない一対一対応
・ペーパーを使った線結び
・~より~個多い(少ない) - step3「等分」
- ・水、ひも、折り紙の2・3・4等分
・余りのないおはじきの等分
・余りのあるおはじきの等分 - step4「一対多対応」
- ・具体物を使った一対多対応
・おはじきを使った一対二・三・四対応 - step5「10の構成、交換」
- ・10の構成
・方眼を使った数の構成
・10をテーマとした数の構成 - step6「数の増減、数のやりとり」
- ・数の増減
・約束による数の増減
・数のやりとり - step7「総合」
- ・総まとめ
難しい課題に取り組む前提として、以上のような基本学習を事物教育・対話教育の方法でしっかり学習する必要があります。その上で、ペーパーを使った繰り返しのトレーニングが意味を持ってきます。自分で物事に働きかけ、試行錯誤し、自分で考える経験を大事にしてください。