週刊こぐま通信
「今何を学習すべきか」数 応用31 置き換え・交換・消去6
2009/10/30(Fri)
前週は、幼小一貫論理育成問題集「置き換え・交換・消去」の中から「何段階かに分けて交換を考えていく問題」を見ていきました。今週は「消去」の問題です。この問題集の中に次のような問題があります。
太郎君と花子さんが持っているものは、どちらかいくつ多いですか。多い方の部屋に多い数だけを描いてください。
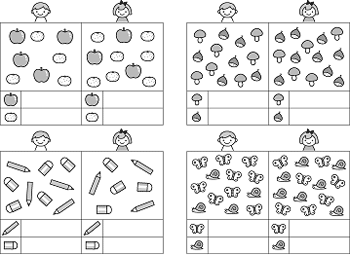

| 解答 | 左上 | 太郎君リンゴに1個、花子さんミカンに3個 |
| 右上 | 太郎君キノコに2個、花子さんクリに3個 | |
| 左下 | 太郎君消しゴムに1個とエンピツに1個 | |
| 右下 | 太郎君チョウチョに2個、花子さんカタツムリに3個 |
消去は、比較対象の中から同じものを取り去り、残っているもの同士を比べる考え方です。上の問題で具体的に考えていきましょう。左上の部屋では、リンゴ3個とミカン4個が共通していますから、これをどちらの部屋からも取ってしまう(消去する)と、太郎君はリンゴが1個、花子さんはミカンが3個残ります。この残った物の数だけ多いことがわかります。同様に右上では、共通しているキノコ5個とクリ6個を取ってしまうと太郎君はキノコ2個、花子さんはクリ3個が多いことがわかります。
この消去の考え方は、本来小学校の文章題にありました。
「エンピツ4本とケシゴム2個を買うと220円です。同じエンピツ6本とケシゴム2個を買うと280円です。エンピツ1本、消しゴム1個の値段はそれぞれいくらですか。」
というような問題です。この問題の考え方は、例えばエンピツ4本とケシゴム2個のセットをAセット、エンピツ6本とケシゴム2個のセットをBセットとしましょう。Aセットの値段は220円、Bセットの値段は280円です。なぜBセットの方が高いのでしょう。それは、AセットとBセットを比べると、消しゴムの数は同じですが、エンピツの数がBセットの方が2本(6-4=2)多くなっているからです。この2本の差が値段の違いの60円(280-220=60)になっています。エンピツ2本分が60円ですから、エンピツ1本は30円(60÷2=30)になります。さらにこれをAセットに戻して、220円からエンピツ4本分の120円(30×4=120)をひいた100円(220-120=100)が消しゴム2個分になります。したがって、消しゴム1個は50円(100÷2=50)になります。
このように小学校の算数の文章題の考え方を幼児向けの問題にしたものが多くあります。これ以外に旅人算的な考え方で行う「飛び石移動」などもそうです。この問題のように両方から同じものを消していくことは、数学的に見れば、2つの数式が等号でつながっている場合、両辺から同じものを取り去ってもその関係は変わらないと言う、同値関係の考え方に通じるものがあります。幼児向けの問題であっても、論理数学的な考え方をトレーニングできるものが今回の例題にようにたくさんあります。そして、この問題集には、この問題をはじめとしていろいろな消去の考え方を使った問題があります。