大きさの違う三角パズルの構成は、まず大きな三角をどこで使うかを考えること

2009年8月6日回答

受験生の皆さまの学習相談に、こぐま会室長がお応えします。

【質問36】
　夏季難問講座で学習した、分割三角パズルによる図形構成があまり良くできません。どのような練習を心掛けたら良いでしょうか。

　三角パズルを使った構成は、図形構成の中でも基本中の基本です。正方形を対角線で4分割した「直角二等辺三角形」を6～10枚使って構成する課題が基本ですが、これまでは同じ大きさの三角パズルでした。ところが、2004年度の雙葉小学校で次のような問題が出されました。

大きい三角パズル2枚と、小さい三角パズル2枚を合わせてできる形に、できない形に×をつける。
※実際に動かせるパズルが大小1枚ずつある。（2004年度）

私の記憶する限り、大きさの違う三角パズルである形をつくるというのは、この問題が初めてだったのではないかと思います。しかも、三角2枚でより大きな三角になるという関係で大きさが設定されていました。これこそが三角パズルの学習ポイントになるところで、「三角と三角でまた三角ができる」という大事な観点が見事に活かされています。

こうした問題の背景を分析し、難問講座では、大きさの違う三角パズルを使った「分割三角パズルによる構成」と題した授業を行いました。ここでは、大小だけでなく、大(2分の1)・中（4分の1）・小（8分の1）・極小（16分の1）の4段階の三角パズルを使った構成の学習をしました。見本と同じ形をつくるわけですが、こうした問題の場合、まず一番大きな三角をどこで使うかが問題です。輪郭のはっきりしているところに使う分には何も問題はありませんが、輪郭のないところに大きな三角を使うことは大変難しい課題になります。例えば、以下のような課題です。

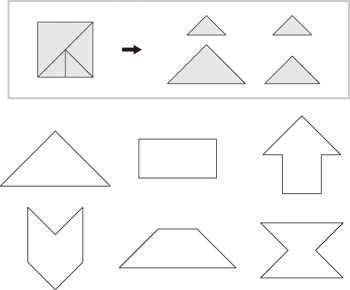
上記の見本では、下の段にある3つの形が難しいようでした。特に右下の課題は子どもたちも苦労していました。

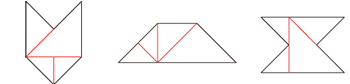
一番大きな三角を使う場所がわかれば、それ以降はだんだん小さな三角を使うようにしていきます。その過程で「三角2つでより大きな三角ができる」という見方が必要になってきます。それが、この図形構成のポイントになるところです。

さて、こうした難しい問題に行きつくまでの三角パズルの練習の仕方は、次のように考えてください。

同じ大きさの三角パズル4～8枚で見本と同じ形をつくる
正方形を2等分した三角1枚と、4等分した三角2枚の3枚を使って見本と同じ形を作る。その際、小さな三角2枚はくっつけると大きな三角1枚になることをいつも意識して行う
大1枚・中1枚・小2枚の三角4枚で見本と同じ形をつくる

この3段階のパズルを練習すれば、大きさの違う三角パズルの基本は身につくと思います。