週刊こぐま通信
「小・中・高 現場教師が語る幼児教育の大切さ」vol.58「ジュニア算数オリンピック 2011 解答・解説」
2011年6月3日（金）
こぐま会小学部長 渋谷 充
今週のコラムは、2011年5月22日（日）に行われたジュニア算数オリンピックトライアルの解答・略式解説の速報をお伝えいたします。（取り急ぎ略式解説をつけましたが、よりエレガントなものができれば随時発表していきます）こぐま会小学部長 渋谷 充
- [総評]
- 問題の難易度はやや易で、問題数も11問で昨年と同じ。数字や言語などを利用した論理問題が9問と図形問題が2問という構成は昨年と同様であるが、図形に関する出題が2問とも算数オリンピックと同問になった（例年は1問）。
平面図形は非常にシンプルで難しい。図形問題が例年より思考時間がかかる分、論理問題に関する思考時間をなるべく抑えた設問になった。特に【問題10】は暗算が得意な生徒には1分とかからなかったのではないか。（下記の解説では、生徒ができるだけ思考時間を短くするよう絞り込みを行ってみた。）さらに【問題7】が条件ミスのため取り消しになったことを考えれば、参加生にとって勝負どころの問題は実質8問程度になったと思われる。
その中で、【問題6】や【問題8】は良問。どちらも、数学的思考力の根本になるような試行錯誤を要する。【問題6】は特異点を見つける設問であるが、果ては関数論、整数論などに結びつく源になりうる。【問題8】は3けたの整数に一定の操作を加えて新たな整数を作るという設問。操作の方法には違いはあれど、よく見る設定である。この類の問題が衰退しないのは、やはり根本的な力を身につけるためには非常に大切な考え方が含まれるからである。いずれの問題も、正答した生徒は3分類できると思う。(1)たまたま当たったレベル、(2)途中まで試行錯誤して後は直感というレベル、(3)理論的に導いたレベル。(1)と(2)の生徒はテスト後もしっかりこの問題を復習して、「絶対この答えになる」ということを第三者に説明できるところまでがんばろう。現状では(2)の生徒がほとんどであると思われる。途中からは“感”で答えを出すという方法は、算数・数学では非常に大切な能力だ。しかしテストが終わり、勉強をする目的から“合格するための”という要素が一時的にでも薄まっている時期は、このような問題をたとえ数時間かかっても成し遂げるという勉強法に切り替えるべきで、その道を通らずして算数力が身につくことはない。
【問題5】は昔ながらの魔法陣の問題。陳腐ではあるが、生徒がこの問題を本当にあっさりこなすかは別。この問題を即答できるぐらいに算数に精通していることを求められるのだから、改めてオリンピックのレベルの高さをうかがい知れる。【問題7】も（もしミスがない問題ならば）論理的思考過程が面白い。
【問題2】【問題4】【問題10】についての下記に示した解説では、ことあるごとに偶奇による必要条件をもとに絞り込みを行っている。整数問題の基本中の基本として偶奇に関する系は、必ず必要な概念である。
【問題3】や図形問題は前回コラム(vol57.「算数オリンピック 解答・解説」)参照。
- [問題解答・略式解説]
- 以下には各問の試行錯誤度を3段階で示している。
【問題1】 A･･･1 B･･･8 C･･･1 D･･･1 E･･･4 F･･･7 G･･･1
試行錯誤度
Aが１であること、Bが8であることがすぐわかる。例からもわかるように別のアルファベットが別の数字を表すわけではないので、C、Dを1と決定できる。E、F、Gは容易に決定する。
【問題2】 (ア)･･･4g [イ]･･･3g [ウ]･･･1g [エ]･･･5g (オ)･･･2g
試行錯誤度
右側のてんびんから [イ] ＜ [エ] なので、両側に(ア)をのせても大小関係は変わらず
(ア)＋[イ] ＜ (ア)＋[エ] となる。左側のてんびんと比べると [ウ] ＜ (ア) であることがわかる。
(ア)は偶数（4g、2g）なので、[ウ]は5gではないことがわかる。同時に[イ]も[エ]より小さいことから、[エ]が5gであることがわかる。左側のてんびんから[ウ]が3gでないことが簡単にわかるので、[ウ]を1gとして、(ア)が4gのとき成立することを確認する。
【問題3】 (ア)･･･7 (イ)･･･4
試行錯誤度
並べられているカードから、あるカードが「～でなければならない」のように、初期条件をある程度しぼるだけで下の図のようになる。また、下図には座席に対してA～Dの記号をふり、カードには番号をつけた。
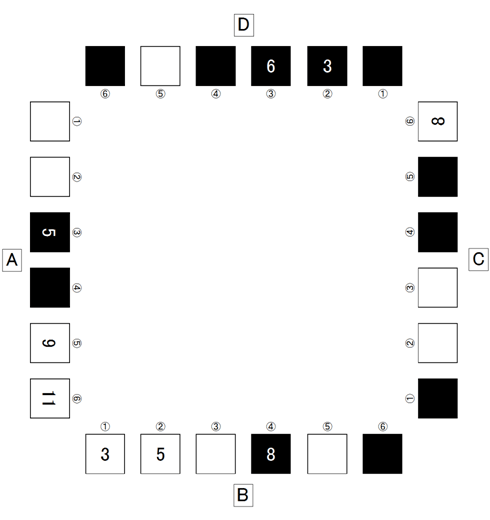
ここで解答を導く論理の一例を紹介する。
- Dの(1)、Cの(1)(4)は黒の0，1，2である。また、Cは(1)(4)の間に白が2枚。
⇒ Cの(1)(4)がそれぞれ黒の0，2。Dの(1)は黒の1。Cの(2)(3)は白の0，1。Aの(1)(2)がそれぞれ白の2，4。Cの(5)は黒の4 - Bの(3)(5)、Dの(5)は白の6，7，10のどれか。
⇒ この中でBの(5)は10でなければならない。Bの(6)は黒の11 - Dの(6)、Aの(4)は黒の9，10。Dの(4)が黒の7。Dの(5)、Bの(3)が白の6，7
⇒ Bの(3)が6。Dの(5)が7。Dの(6)が10。Aの(4)が9。
【問題4】 A･･･[4][5][8] B･･･[2][6][7] C･･･[1][3][9]
試行錯誤度
Cが奇数の一番大きいカード9を持ち、カードの合計が一番小さい。さらに、どの2人もカードを1枚交換すると合計を等しくすることができることから、A，B，Cの偶奇が一致する必要がある。このことから、Cの残り2枚はどちらも奇数。また、カードの合計の平均が15であることからCのカードの和は15未満である。
よって、Cは[1][3][9]、A，Bのカードはどちらも[偶][偶][奇]の組み合わせ。
実際は直感で並べたほうがはやい。
【問題5】 14
試行錯誤度
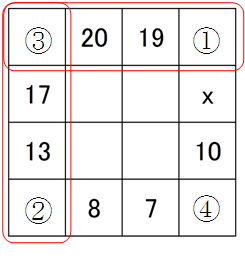
赤線枠の合計が等しいことから、(1)と(2)の差は(3)には依存せず、20＋19＝39と17＋13＝30から、9となる。
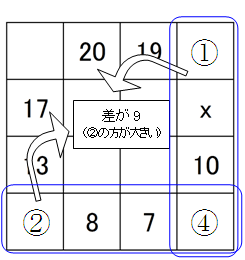
続いて、右図のように青線枠の合計も等しい。同様に差を考慮すると(4)には依存せず、
8＋7＝15 15＋9＝24 24－10＝14
【問題6】 クで8
試行錯誤度
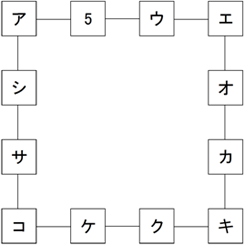イの5をスタートとして、差が1および2になり、1～12の数字を1度だけ使用することを許して1周することを考える。下の(例)のように差が1になる数字を一度使用すると、次には差が2の数字を増減方向をいれかえて使用しなければならない。つまり、差が1の数字を使用できる可能性があるのは、1や12などの折り返し地点のみである。
(例)
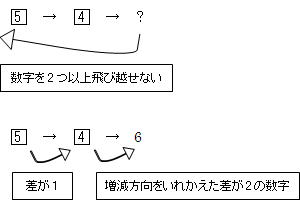
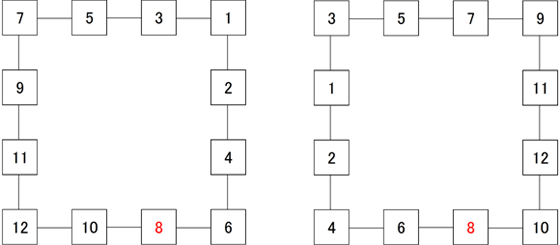
つまり、1と12以外を増減の切り替えポイント（極値）とすることができなく、かつ差が1の数字を使用できるのは1か12に接触している場合のみ。以上から下の様な2通りのマスの埋め方が考えられる。
【問題7】 マーク･･1でB型 ケン･･3でA型 ジョン･･5でB型 サムス･･4でA型 タロウ･･2でA型
試行錯誤度
条件からマークとジョンは1か5でかつどちらも同型。サムスの発言から、A型ロボットが1か5をつけている可能性が否定され、1と5はB型となる。また、残りの2，3，4の中で、ケンの発言からケンは3の数字をつけていて、2と4がA型になることがわかる。同時にサムスが4、タロウが2であることがわかる。最後にタロウの発言（「ボクの次に小さいロボットはA型ロボットです。」に訂正された。）から3のケンがA型であることがわかる。
【問題8】 999,981,972,963,954
試行錯誤度
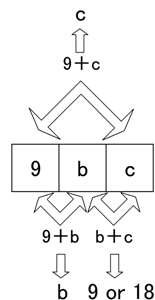もとの整数の百の位、十の位、一の位の数字をそれぞれa , b , c とすると、※1もとの3けたの整数においては少なくともa ≧ b ≧ cとなっていなければならない。また、題意よりa , b , c のうちa = 9の場合のように、もとの整数が【9bc】となる※2右図のような性質のものを5つ見つけるだけで十分ともいえる。つまりb+c=9または18になる組み合わせなので、b≧c を考慮して
( b , c ) = ( 8 , 1 ), ( 7 , 2 ), ( 6 , 3 ), ( 5 , 4 ), ( 9 , 9 ) の5つとなる。
ちなみに、右図はやや甘い条件制限だけで考えたので9+b=bとして候補を絞り込んでいるが、厳密には( b , c ) = ( 9 , 0 )のように上記や右図の条件を満たしているが、吟味して不適切なものも含まれているので丁寧に考えたい。
| ※1 | 例えばもとの3けたの整数が285のように十の位の数がもっとも大きい場合、2つの位の各和を大きい順にいれかえてできた整数がもとの整数と同じになることはありえない。よって、このような必要条件で絞り込んだほうが考える場合が少なくてすむ。 |
| ※2 | b=0やc=0のときはもちろん9+b=bや9+c=cとなるが、b+9≧10, c+9≧10のときも9+b=bや9+c=cとなっている。 |
【問題9】 算数オリンピック【問題11】と同問
試行錯誤度
→前回コラム(vol57.「算数オリンピック 解答・解説」)参照【問題10】 62341
試行錯誤度
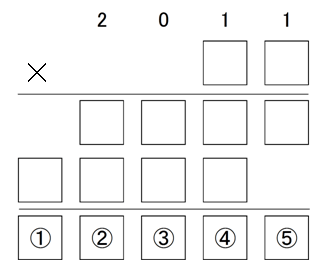2011×[a] の計算過程を考えて、[a] の値の候補を絞り込む。[a]=1～10ではないことは容易にわかる。続いて[a]=11～49（答えが5桁）の範囲について考える。
右のような筆算の形から、次のようなことがわかる。
- 3つの連続した順方向の整数がはいる可能性があるのは、(1)(2)(3)、(2)(3)(4)、(3)(4)(5)の3箇所
- (2)は偶数（a＝11～49）
- (3)は1,2,3（(4)からの繰り上がりとともに）と数字が増えていく。
- (5)は[a]の一の位と同じ数
よって、(3)による場合わけを考える。
| i. | (3)が1のとき、 | (3)(4)(5)が123になることはない。 [a]=13で確認 |
| ii. | (3)が2のとき、 | (2)(3)(4)が123になることはない。 (2)が偶数 |
| (3)(4)(5)が234になることはない。 [a]=14で確認 | ||
| iii. | (3)が3のとき、 | (1)(2)(3)が123になることはない。 (3)が3なので、(1)はすでに1ではない。 |
| (2)(3)(4)が234になる。 [a]=31 のとき 62341 | ||
| (3)(4)(5)が345になることはない。 可能性として [a]=35 が考えられるが、[a]=31 より考慮するまでもない。 |
【問題11】 算数オリンピック【問題9】と同問
試行錯誤度
→前回コラム(vol57.「算数オリンピック 解答・解説」)参照