週刊こぐま通信
「今何を学習すべきか」推理 いろいろなゲーム3 応用2 オセロゲーム(2)
2007/09/07(Fri)
前回に引き続き「オセロゲーム」です。今回はやや難しい問題について見ていきたいと思います。「ひとりでとっくん79 ゲームブック2」に次のような問題があります。(問題)
とのどちらか多い方が勝ちになります。今はが勝っています。が勝つように空いているお部屋にエンピツで1つだけを描いてください。
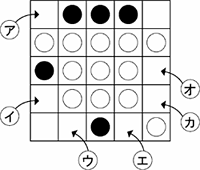
前回はより多くがに裏返る場所を探すだけでよかったのですが、今回はが裏返った後のとそれぞれの数を考えなくてはなりません。しかもが置ける場所はア~カまで、いくつもあります。それぞれの場所にを置いた時の結果は次の通りです。
| アに置いた場合 | 7個 | 11個 | (の勝ち) | ||
| イに置いた場合 | 8個 | 10個 | (の勝ち) | ||
| ウに置いた場合 | 9個 | 9個 | (あいこ) | ||
| エに置いた場合 | 9個 | 9個 | (あいこ) | ||
| オに置いた場合 | 11個 | 7個 | (の勝ち) | ||
| カに置いた場合 | 8個 | 10個 | (の勝ち) |
つまりオに置いた場合のみの勝ちになります。
この問題を解くポイントはふたつあります。ひとつはを置いた後のとの数を正確に数えることです。を数えてみましょう。まずどこかのマスにを置いてみて、それによってに裏返るの数を数えます。この場合1つの方向だけでなく、斜めも含めたいろいろな方向に目を配らなくてはなりません。そして、その数とはじめから置いてあるを足して、全部でいくつになるかを考えます。次にを数えてみましょう。これは以上に難しいと思います。それは、どのが裏返ってになったのかをきちんと判断して、残りのの数を考えなくてはならないからです。場所と数の正確な理解が必要とされます。
次のポイントは、を置くことができる場所が、ア~カまで6ヶ所あることを認識することです。もしも、2、3箇所しか見つけることができなかったら、他の見落とした場所に正解があるかもしれません。子どもはひとつの問題を解決するとそれでできたものだと思い、他の場合を考えることをあまりしません。一つ一つの場所をもれなくチェックして、有り得る場合を全て考えられるようにしてください。最近の小学校入試では、こうしたいろいろな場合について考えるような複雑な問題も多く出題されています。
相手と対戦するゲームにおいては、いろいろな場面で次の1手を考えなくてはなりません。どこに置いたら自分が一番有利になるかを考えることは、ゲームに勝つことが動機付けになりますから、子どもは一生懸命に行います。ご家庭でもゲームの途中で立ち止まって、お子さまに次の1手を考えさせることによって、さまざまな問題場面を解決していく洞察力を身につけてさせてください。