「考える力を求める入試問題(1)」

第708号　2020年2月7日(金)
こぐま会代表　久野泰可

　昨年秋の2020年度入試で出題された問題もほぼ聞き取り収集ができました。「どんな問題が出されたのか」「難易度はどうであったのか」「どんな能力が求められていたのか」などの分析もほぼ終了しました。そこで、これから数回にわたって2020年度の入試問題の中から典型的な問題を紹介し、学校側が求める幼児期の終わりまでに育ってほしい「考える力」を解説いたします。

1. シーソーのつりあい: 上のお部屋を見てください。野菜をシーソーにのせて重さをくらべました。タマネギ1個はナス2個とつりあいます。ナス1個はトマト3個とつりあいます。問1：真ん中のお部屋を見てください。タマネギ1個とつりあうにはトマトを何個のせたらいいですか。その数だけ右のお部屋に青いをかいてください。問2：下のお部屋を見てください。それぞれシーソーはどちらが重くなりますか。重くなるほうに赤いをつけてください。

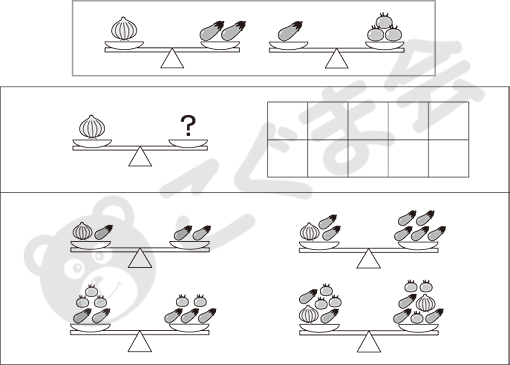
問1の「玉ねぎ1個とつり合うにはトマト何個を載せたらいいですか」という問題は、玉ねぎとトマトの関係をナスを仲立ちとして考える問題です。こうした「置き換え」をともなう問題を解くためには、まず基礎的な練習が必要です。それは、仲立ちを介さない問題の練習です。この問題に即していえば、最初に、玉ねぎとナスの関係を学習し、次にナスとトマトの関係を学習します。例えば、「玉ねぎ3個はナス何本とつり合いますか」を聞いたら逆に、「ナス8本は玉ねぎ何個とつり合いますか」というように一方向だけでなく、逆からも聞きます。こうした問題は、私たちの学習では一対多対応と呼んでいて、将来のかけ算の考え方、わり算の考え方（逆からの問いかけ）につながる大事な内容です。ここをまずしっかりとやらなければなりません。その上で、玉ねぎとトマトの関係をナスを仲立ちとして（置き換えて）考える問題です。この何かに置き換えて考えるという発想が難しいのです。この置き換えの発想は、年中児の現段階では難しいと思いますが、いろいろな経験を積んで年長の夏ごろには解決できるようになるはずです。問題は学ぶプロセスを間違えないようにすることです。特に置き換えの問題は、数の領域で学習する「交換」の問題と関連づけて学習するのが良いと思います。ルールを決めた交換ゲームをやるのが一番分かりやすいと思います。こぐま会では銀行ゲームなどをやって、実際の場面で置き換えを含めた交換の経験を積んでいます。
問2はどちらが重くなるかを判断する問題ですが、解き方はいろいろあります。ここでも何かに置き換える発想が求められますが、もうひとつ、左右両方から同じものを下ろしても（実際には線で消す）重さの関係は変わらないという考え方が理解できれば、残った少ない数で比較することができます。いずれにしても何かに置き換えて考える「交換」の問題につながる内容です。

2. 数の増減とやりとり

クマ、イヌ、パンダが持っているりんごの半分の数を、同時に矢印の方にいる動物にあげます。2回、同時に矢印の方にいる動物にりんごをあげたとき、パンダが持っているりんごの数はいくつになりますか。下のお部屋にをつけてください。

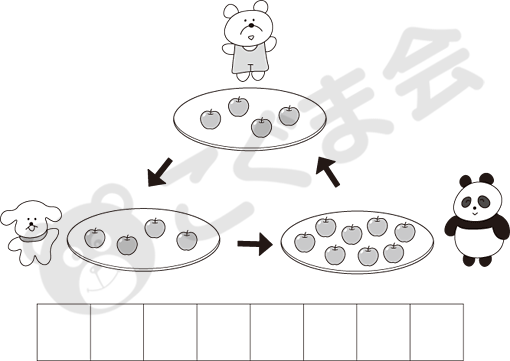
クマとイヌとパンダが持っているりんごを、約束に従って2回受け渡しをしたときに、パンダのりんごの数がいくつになるかという問題です。この問題が子どもたちにとって難しいのは、三者でやり取りする関係をしっかり理解できるかどうかです。問題の意図はすぐにつかめますし、ゲーム化してもできる問題です。相手からもらうという行為と、自分からもう1人の相手にわたすという「もらう行為」と「あげる行為」の動いていく関係を踏まえて、数がどのように変化していくかを考えなければなりません。それも決まった数をやり取りするのでなく、もらう場合もあげる場合も「持っている数の半分」を移動させなければなりません。例えばパンダに注目した場合、今持っている8個のうち半分の4個をクマにあげ、イヌの持っている4個の半分をイヌからもらいます。その結果1回の移動で、6個のりんごを持つことになります。2回目は、1回目の移動でイヌは4個になり、クマは6個になっているため、それを踏まえて受け渡し後の数の変化を考えなければなりません。幸いイヌからもらう数は、2回目も4個の半分の2個です。パンダのほうは6個のうち3個をクマにあげ、残りは3個になりますから、イヌからもらう2個と合わせて5個になり、これが答えとなります。もらう行為とあげる行為の2つの視点を同時に考えながらりんごをやり取りするこの課題は、2人での数のやり取りと違ってかなり難しいと思います。順序立てて考えるという意味で、考える力を問う良い問題だと思います。

3. しりとり

（れい）のお部屋を見てください。ここにある絵はしりとりでつながります。「つき − きつね − ねずみ − みみ」とつながって、最後になった「みみ」にがついています。

同じように横に並んでいる絵をしりとりでつないだとき、最後になる絵にをつけてください。

こちらは、子どもにとっては日常的な言葉遊びである「しりとり」を使って思考力を問う問題です。しりとりの問題にはいろいろなタイプがあります。次の問題はそれが集約されたものです。

4. しりとり

（れい）のお部屋を見てください。リンゴ－ゴリラと、しりとりでつながるものはラッパなので、右のラッパの絵に星のマークがついています。

同じように他の並んでいる3つのお部屋が、しりとりでつながるには、空いている？のお部屋に何を入れたらよいですか。お部屋の下についている印と同じ印を右の絵につけてください。

ここにしりとりに関する典型的な問題があります。

最初が分かっていて後ろにつなげる問題
- -
前の言葉と後ろの言葉が分かっていてそれをつなぐ言葉を捜す問題
- -
真ん中の言葉が分かっていて、前の言葉と後ろの言葉を捜す問題
- -
前にもどって考える問題
- -

※いずれもは分かっていて、にことばを入れる問題

今回紹介した問題は、こうしたしりとりに求められる基本理解を踏まえて、ばらばらな言葉を「しりとり」になるように仕上げる問題です。最初も最後も分からない状態から、言葉をいろいろ組み合わせて「しりとり」になるように完成させる課題は、易しいようでかなり高度な考える力が必要になります。しりとりのルールに従って、進んだり戻ったりする作業を集中して根気強くできるかどうか。入試問題にふさわしい良い問題だと思います。

幼児教育が注目され、幼児教育の課題として「幼児期の終わりまでに育ってほしい10の姿」が公表されました。私たちが一番注目している知育に関する課題については、10項目の中で、

6. 思考力の芽生え
8. 数量や図形、標識や文字などへの関心･感覚
9. 言葉による伝え合い
10. 豊かな感性と表現

といった表現がされていますが、あまりにも漠然とした言い回しに現場は混乱しています。「思考力の芽生え」で何を言おうとしているのでしょうか。「数量や図形、標識や文字などへの関心・感覚」で何を言おうとしているのでしょうか。こんなあいまいな議論をしても、教育の質は深まりません。挙句の果て、最近では「10の姿」は到達目標でなく「望ましい方向性だ」とここでも曖昧な言い方をしています。こんな状況ですから、日本の幼児教育においては、「正しい知育」は始まりそうにありません。その結果、遊び保育に飽き足らなくなると、知識のつめ込み、読み・書き・計算が始まるのです。幼児期にこそ身につけなければならない、「学ぶ楽しさ」「学ぶ姿勢」「考える力」が育つはずはありません。教育の始まりとして一番大事な幼児期の教育です。日本には、数学の専門家も言語の専門家も大勢いるはずです。そういう個別の学問の専門家を大動員して、遠山氏が提案した「原数学」「原言語」の具体的な内容を構築すべき時です。

私は以前、取材を受けた際に、幼児教育の課題を考えるひとつのきっかけとして、小学校の入試問題を参考にして、幼稚園の先生、小学校の先生で何を教育課題にするかを具体的に議論してみたらどうかと提案したことがあります。小学校の入試問題は、具体的であるだけに議論するきっかけになるはずです。もう抽象的な議論を展開している時期ではありません。「幼児教育の学校化」を長年拒否してきた幼児教育関係者の皆さまに、AI社会で生き抜く子どもたちのために、これからの教育課題・到達目標を具体的に示していただきたいと思います。